简单DP

🪁简介

动态规划：DP：Dynamic Programming是算法的设计方法，是一种编程思想，主要用于解决最优解类型的问题。

对于一个DP问题，首先将问题分解，任选一个最优解的子状态分析，与原问题（原状态）有什么关系。

列出状态转移方程，这个尤为重要

🪁详讲

从集合的角度理解
Dp从两个角度考虑

状态表示，考虑清楚用几维表示状态，表示的是哪一个集合，存的数是集合中的哪一个属性
状态计算，如何一步步把每一个状态算出来

🪁状态表示

每一个状态都表示一个集合

因此要考虑，f(i,j) 表示的是哪一个集合，例如背包问题表示的是所有选法的集合

属性：f(i,j) 表示的是一个集合，实际上存的是一个数，这个数是这个集合的某种属性。因此属性一般有三种：max，min，元素数量

集合：表示的是所有选法的一个集合(选哪些物品)
还有满足一些条件，在01背包问题中，条件是从前i个物品选，总体积小于等于题目要求

状态表示 举例：在01背包问题中，f(i,j) 表示从前i 个物品中选，总体积小于等于j选法的集合，存的数是这个集合的每一个选法价值的最大值

🪁状态计算

对应的是集合的划分
如何把当前的集合划分为若干个更小的能算出来的子集，能用前面更小的状态(集合)表示出来

划分方式：是否包含(加入)第i 个物品(第i个物品对结果是否有影响)

划分原则：

  • 不重复：某一个元素不可以属于两个集合(不一定满足)
  • 不遗漏：某一个元素不属于任何集合(必须满足)

举例：在01背包问题中

不包含i 的计算：从 0 ~ i-1 中，总体积不超过j选法的集合，因此最大值是f[i-1][j]
包含i的计算：从 0 ~ i 中，总体积不超过j选法，用状态转移方程转换一下，即是：f[i-1][j-v[i]]+w[i] 为最大值

总体的最大值是 max(f[i-1][j],f[i-1][j-v[i]]+w[i])

🪁优化

DP的优化一般是对动态规划的代码或是方程做一个等价变形

先写出基本的状态，再做优化

🪁01背包问题：

问题描述：有 N件物品和一个容量是 V的背包。每件物品只能使用一次。

第 i件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

基本写法，二维数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <bits/stdc++.h>

using namespace std;

const int N = 1005;
int v[N];    // 体积
int w[N];    // 价值
int f[N][N]; // f[i][j], j体积下前i个物品的最大价值
// i 表示第几个物品  j 表示还有多少体积

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
        {
            f[i][j] = f[i - 1][j]; //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if (j >= v[i])         // 能装，需进行决策是否选择第i个物品
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }
    
    cout << f[n][m] << endl;
    
    return 0;

优化版，利用 滚动数组+倒序查找
为什么一维情况下枚举背包容量需要逆序？
在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。

简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」，逆序则不会有这样的问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int v[N]; // 体积
int w[N]; // 价值
int f[N];//N 件物品，背包容量j下的最优解

int main()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)//倒序比较
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;

}

🪁一道DP题目

🚀传送点: 1015. 摘花生

题目描述

Hello Kitty想摘点花生送给她喜欢的米老鼠。

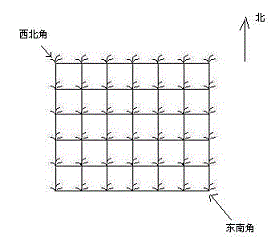
她来到一片有网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

1.gif

输入格式

第一行是一个整数T，代表一共有多少组数据。

接下来是T组数据。

每组数据的第一行是两个整数，分别代表花生苗的行数R和列数 C。

每组数据的接下来R行数据，从北向南依次描述每行花生苗的情况。每行数据有C个整数，按从西向东的顺序描述了该行每株花生苗上的花生数目M。

输出格式

对每组输入数据，输出一行，内容为Hello Kitty能摘到得最多的花生颗数。

数据范围

1≤T≤100,
1≤R,C≤100,
0≤M≤1000

样例

输入样例：
1
2
3
4
5
6
7
2
2 2
1 1
3 4
2 3
2 3 4
1 6 5
输出样例：
1
2
8
16

🪁思路

1.状态表示
集合：定义为从f[i][j]为(1, 1)到达(i, j)的所有方案

属性：最大值

2.状态计算 (i, j)从(i-1, j)即上方过来； (i, j)从(i, j-1)即左方过来

3.空间压缩
f[i][j]只需要用到这一层和上一层的f元素，所以可以压缩成滚动数组。在此之上，还可以直接压缩成一维数组。

🪁C++ 代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<iostream> 
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=110;
int w[N][N];//原数组
int f[N][N];//状态数组
int t;
int main(){
	int r,c;
	scanf("%d",&t);
	while(t--){
	scanf("%d%d",&r,&c);
	for(int i=1;i<=r;i++)
		for(int j=1;j<=c;j++){
			scanf("%d",&w[i][j]);
		}
	memset(f, 0, sizeof f);//在 f 这个数组里面 sizeof f 的长度中填入 0 ， 相当于清空结果数组。不清空也是可以得到答案，
	for(int i=1;i<=r;i++)
		for(int j=1;j<=c;j++){
		f[i][j]=max(f[i-1][j],f[i][j-1])+w[i][j];//状态分割 分为上方过来的和左方过来的 取最大
		}
	printf("%d\n",f[r][c]);//遍历f[1][1]~f[r][c] f[r][c]即为最后数
	}
	
	return 0;
}

🪁 其他DP题目: